Fortran Program For Secant Method Advantage
Here are the Bisection Method formulas xm = (xl+xu)/2 I'm not convinced that you understand what the above means. X L - Lower (left) endpoint of an interval x M - Midpoint of an interval x U - Upper (right) endpoint of an interval a) If f(x L)*f(x M) 0, the graph of the function does not cross the x-axis between x L and x M, so we should look in the other half of the interval - in [x M, x U]. If so, USE THE SAME VALUE FOR x U (i.e., don't change x U), but reset x L to x M.
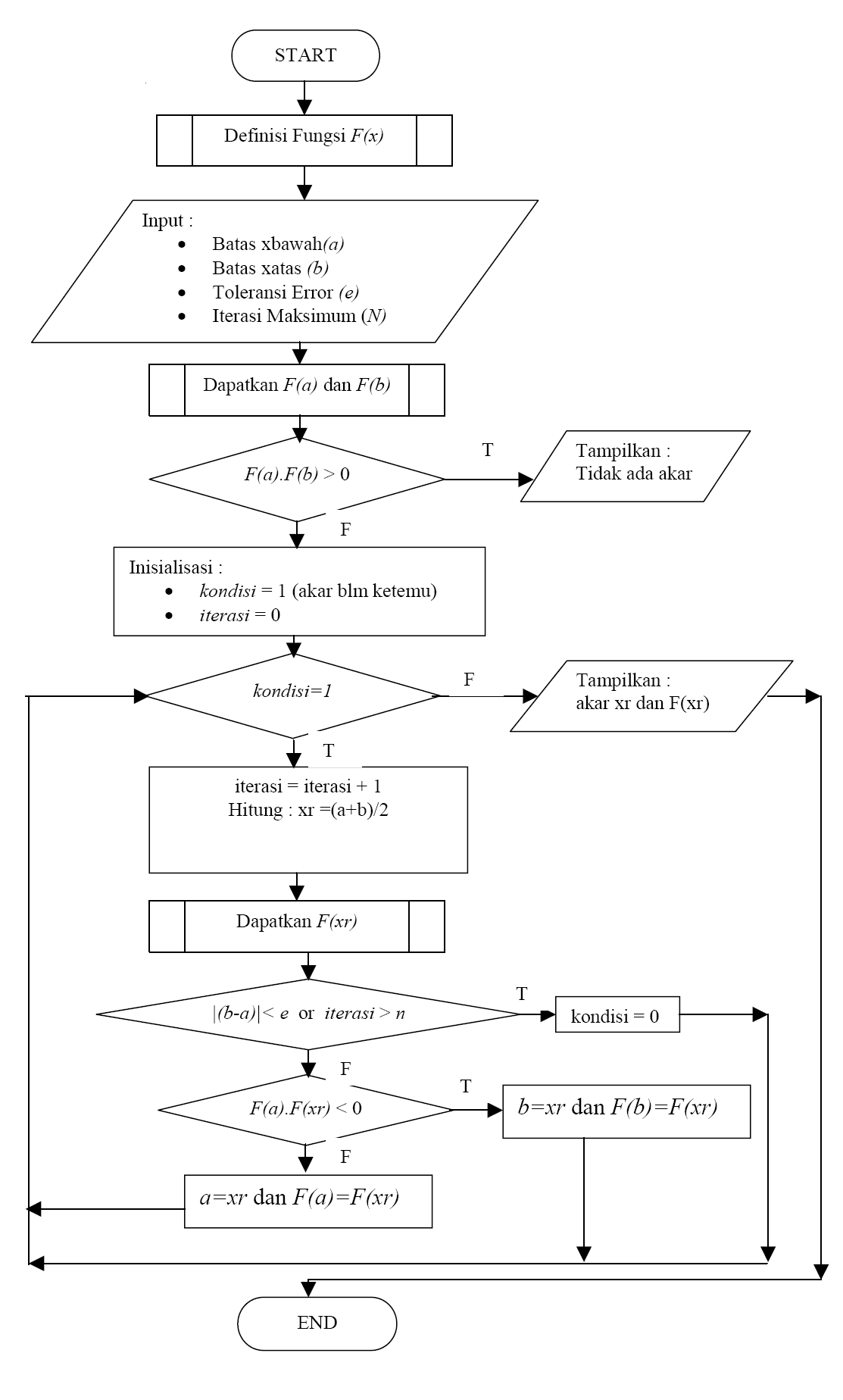
3.2 Bisection. This is the simplest method for finding a root to an equation. As we shall see, it is also the most robust. One of the main drawbacks is that we need two initial guesses xa and xb which bracket the root: let fa = f(xa) and fb = f(xb) such that fa fb fa. They will be catalogued here, in the order in which the relevant methods have appeared in the main text of the chapter. Dowell and Jarratt (1971) and King (1984) give programs for the Illinois method (see Section 7.2 of this chapter). They are in Algol and Fortran respectively. Several programs for the bisection method are.
Your code should NOT include x U = x U. At each step for a) or b), we are shortening the interval by half its length, so that we eventually find the root. C) If f(x L)*f(x M) = 0 then either f(x L) = 0 or f(x M). Drivers Conexant Fusion 878a Win Xp.
Female Mugen Chars Download Free. There's probably an assumption that f(x L) ≠ 0 and f(x U) ≠ 0, but you didn't show it in the attachment you posted.
Contents • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • [ ] with Ada. Text_Io; use Ada. Text_Io; procedure Roots_Of_Function is package Real_Io is new Ada. Translation of: print_roots = (f, begin, end, step ) -># Print approximate roots of f between x=begin and x=end, # using sign changes as an indicator that a root has been # encountered. X = begin y = f (x ) last_y = y cross_x_axis = ->(last_y 0 ) or (last_y >0 and y # Smaller steps produce more accurate/precise results in general, # but for many functions we'll never get exact roots, either due # to imperfect binary representation or irrational roots. Step = 1 / 256 f1 = (x ) ->x *x *x - 3 *x *x + 2 *x print_roots f1, - 1, 5, step f2 = (x ) ->x *x - 4 *x + 3 print_roots f2, - 1, 5, step f3 = (x ) ->x - 1.5 print_roots f3, 0, 4, step f4 = (x ) ->x *x - 2 print_roots f4, - 2, 2, step output >coffee roots.coffee ----- Root found at 0 Root found at 1 Root found at 2 ----- Root found at 1 Root found at 3 ----- Root found at 1.5 ----- Root found near -1.4140625 Root found near 1.41796875 [ ]. Output: Root found at 8.6218e-16 Root found at 1.000016 Root found at 1.998914 [ ]% Implemented by Arjun Sunel - module (roots ).
- export ( [main / 0 ] ). Main ( ) ->F = fun ( X ) ->X * X * X - 3 * X * X + 2 * X end, Step = 0.001,% Using smaller steps will provide more accurate results Start = - 1, Stop = 3, Sign = F ( Start ) >0, X = Start, while ( X, Step, Start, Stop, Sign, F ). While ( X, Step, Start, Stop, Sign, F ) ->Value = F ( X ), if Value == 0 ->% We hit a root: format ( 'Root found at ~p~n', [ X ] ), while ( X + Step, Step, Start, Stop, Value >0, F ); ( Value% We passed a root: format ( 'Root found near ~p~n', [ X ] ), while ( X + Step, Step, Start, Stop, Value >0, F ); X >Stop ->: format ( ' ); true ->while ( X + Step, Step, Start, Stop, Value >0, F ) end. Output: Root found near 8.6218e-16 Root found near 1.000016 Root found near 2.998915 ok [ ] PROGRAM ROOTS_FUNCTION!VAR E,X,STP,VALUE,S%,I%,LIMIT%,X1,X2,D FUNCTION F(X) F=X*X*X-3*X*X+2*X END FUNCTION BEGIN X=-1 STP=1.0E-6 E=1.0E-9 S%=(F(X)>0) PRINT('VERSION 1: SIMPLY STEPPING X') WHILE XLIMIT% THEN PRINT('ERROR: FUNCTION NOT CONVERGING') EXIT END IF D=(X2-X1)/(F(X2)-F(X1))*F(X2) IF ABS(D). Output: Root (to 12DP) Max. Error 0.08 1e-06 1.16 1e-06 2.34 1e-06 Note that the roots found are all near misses because fractional numbers that seem nice and 'round' in decimal (such as 10^-6) often have some rounding error when represented in binary.
To increase the chances of finding exact integer roots, try using an integer start value with a step value that is a power of two. -- Main procedure print ( 'Root (to 12DP) tMax.